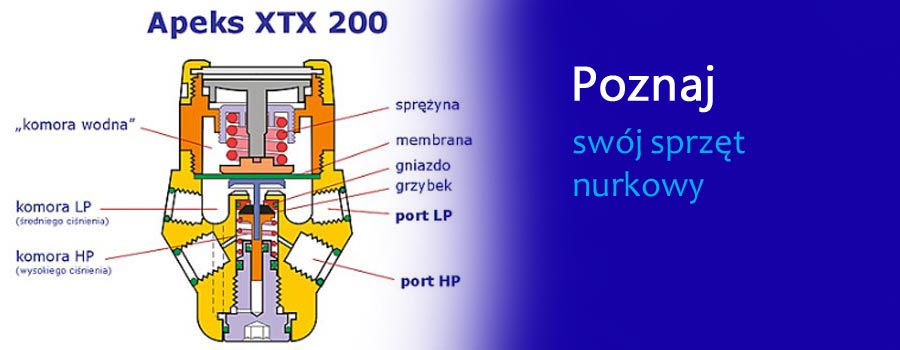
Jak zapisać się na kurs nurkowania!
Kursy nurkowania prowadzimy w Krakowie. Zależy ci na szybkim terminie - skontaktuj się z instruktorem
Tel.: (+48) 501 627 846. lub e-mail. Zawsze możesz zadzwonić i zapytać. Preferujemy kontakt telefoniczny. Więcej.
Jak widzimy pod wodą
fizyka nurkowania

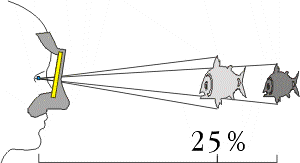
Obraz, tworzony pod wodą przez "gołe" oko jest nieostry. Wynika to z innego niż na powierzchni kąta załamania promieni światła wpadających do gałki ocznej, które nie ogniskują się na siatkówce, ale poza jej płaszczyzną. Założenie maski lub okularków pływackich umożliwia ostre widzenie (światło wpada do oka z środowiska powietrznego). To jednak nie wszystko, promienie światła przechodzące przez szybkę maski uginają się tworząc obraz przedmiotów:
- powiększony o 33% (1/3) - z tego powodu ryby i wszystkie przedmioty wydają się większe, niż są w rzeczywistości.
- i przybliżony o 25% (1/4) - dlatego jeżeli próbujemy po coś sięgnąć, okazuje się, że ręce mamy zbyt krótkie.